z2+c+si
si = -1, 1, -1, 1, …
C3.02: 0.000323, 0.777540, Zoom = 40
Sequence Fractals Part I #28


z2+c+si
si = -1, 1, -1, 1, …
C3.02: 0.000323, 0.777540, Zoom = 40

z2+c+si
si = -1, 1, -1, 1, …
Center:C3.00 -0.028857, 0.822581, Zoom = 5000

z2+c+si
si = -1, 1, -1, 1, …
Center:C3.00 -0.028857, 0.822581, Zoom = 100
30 three cycles
C3.00: -0.028857, 0.822581
C3.01: -0.028857, -0.822581
C3.02: 0.000323, 0.777540
C3.03: 0.000323, -0.777540
C3.04: 0.123345, 0.786543
C3.05: 0.123345, -0.786543
C3.06: 0.123768, 0.684849
C3.07: 0.123768, -0.684849
C3.08: 0.256240, 1.261825
C3.09: 0.256240, -1.261825
C3.10: 0.456809, 1.544145
C3.11: 0.456809, -1.544145
C3.12: 0.475692, 1.211907
C3.13: 0.475692, -1.211907
C3.14: 0.543537, 1.408400
C3.15: 0.543537, -1.408400
C3.16: 0.729946, 1.274941
C3.17: 0.729946, -1.274941
C3.18: 0.731182, 1.053796
C3.19: 0.731182, -1.053796
C3.20: 0.774380, 1.836743
C3.21: 0.774380, -1.836743
C3.22: 0.802629, 1.829248
C3.23: 0.802629, -1.829248
C3.24: 0.827269, 1.802481
C3.25: 0.827269, -1.802481
C3.26: 0.828125, 1.397028
C3.27: 0.828125, -1.397028
C3.28: 0.855612, 1.812967
C3.29: 0.855612, -1.812967

z2+c+si
si = -1, 1, -1, 1, …
Center:C2.04 (0.633096, 1.288065), Zoom = 16

z2+c+si
si = -1, 1, -1, 1, …
Center:C2.04 0.633096, 1.288065, Zoom = 16
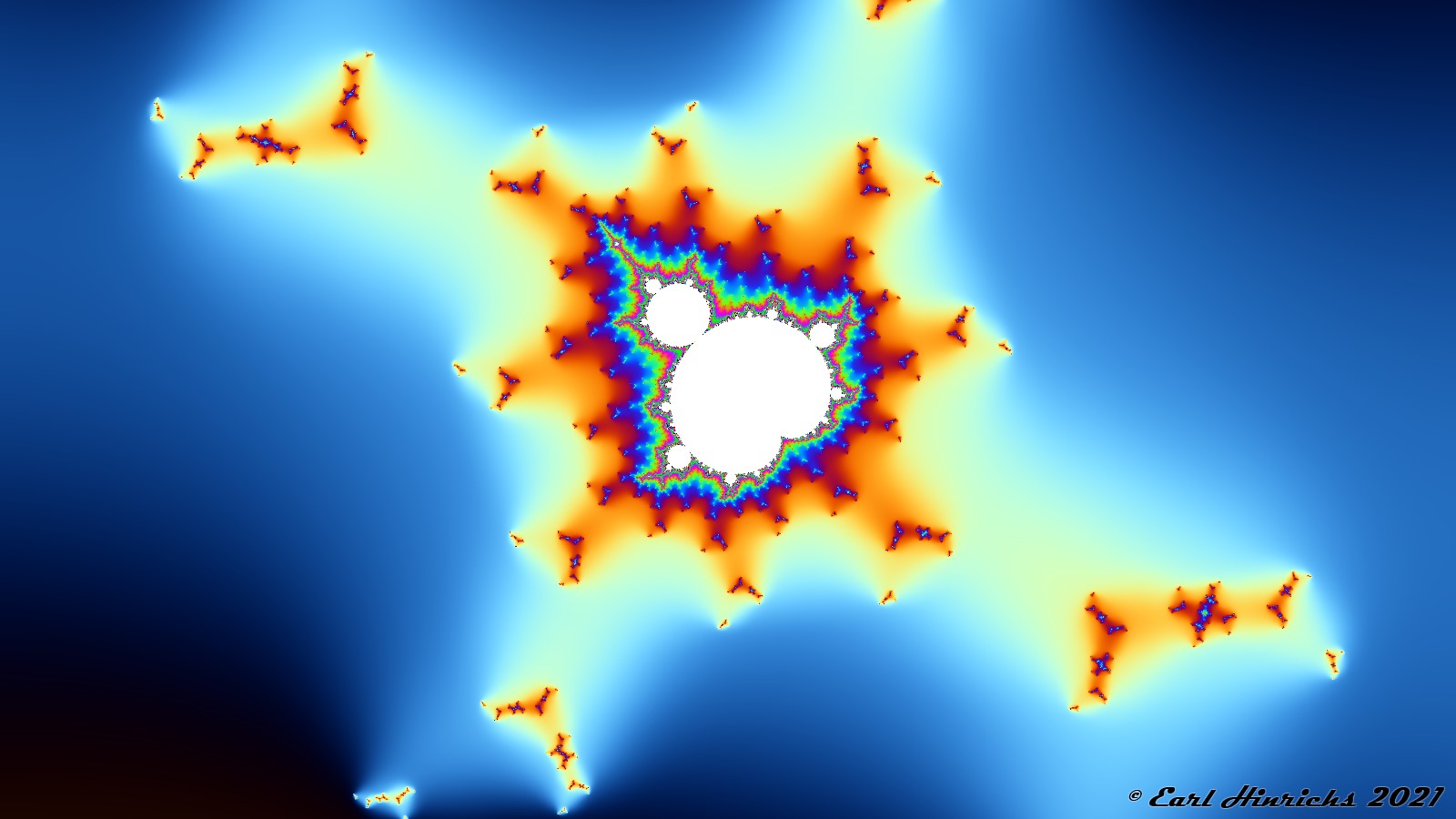
z2+c+si
si = -1, 1, -1, 1, …
Center: C2.00: 0.053427, 0.781326, Zoom = 40

si = -1, 1, -1, 1, …
Center: C2.00: 0.053427, 0.781326, Zoom = 16
6 two cycles
C2.00: 0.053427, 0.781326
C2.01: 0.053427, -0.781326
C2.02: 0.633096, 1.288065
C2.03: 0.633096, -1.288065
C2.04: 0.813477, 1.815442
C2.05: 0.813477, -1.815442
Everything is reflected across the real axis. C2.01 is exactly the same, just flipped vertically. So I will ignore everything going on in the bottom half of the complex plane.

si = -1, 1, -1, 1, …
Center: C1.00: 0.500000, 1.322876, Zoom = 0.8
z0 = 0 is a critical point and will again be the default starting point. The other two critical points will be ignored without guilt. They just bring us back to the sequence starting 1,-1…, about which we already know more than we ever wanted to know.
Fixed points are found when f(0,c) = 0. so c = = 0.5 ± 1.322876i.
2 fixed points
C1.00: 0.500000, 1.322876
C1.01: 0.500000, -1.322876
I will start naming named points with a leading letter to avoid confusion with decimal numbers.

si = -1, 1, -1, ,1, …
Center:0+0.i, Zoom = 0.25,
Variable plane (Julia), c0 = 0
Here is a picture of the Julia set for the new sequence (starting with -1). It is disconnected, has interior, yet is not dust.
If you are reading these posts you probably know Julia sets. But just in case, here is the wiki definition: Julia set. The picture is the Filled Julia Set. The actual Julia set is the boundary around the white areas.
Stepping way back to the basics.(I should have explained this a long time ago, I just assumed it was obvious.) We have a complex function in two variables, f(z,c). I like this view, it has symmetry, calling out both variables avoids confusion. Equivalently, and traditionally, we are looking at a family of complex functions fc(z), indexed by a complex value, c. z is the variable and c is the parameter. Fix two numbers c0, z0, and define a sequence of numbers by iteration, zi+1=fc0(zi), called an orbit. The question is how does this orbit behave in the limit. The simplest dichotomy is the orbit goes to infinity or it does not. In all of the pictures the non-escaping points are colored white (traditionally they are black, I am just changing things up to be different). The escaping points are colored (approximately) by how quickly the orbit rushes off to infinity.
In the previous pictures in this series, z0 = 0 (usually) and c0 depends on the pixel. A linear map maps pixel coordinates to complex numbers. Such pictures could (and probably should) be called “Non-escaping parameter plane” pictures. For the function family z2+c, this is the Mandelbrot set.
In today’s picture the c value is fixed, in this case c0 = 0, and the pixels are mapped to the complex plane for the starting z0 value. z is the variable so these are “Non-escaping variable plane” pictures.

si = 1, -1, 1, -1, …
Center:0+0i , Zoom = 0.25
Way back at the start Sequence Fractals Part I #1 we had these definitions:
f0(z,c) = z2+c+1
f1(z,c) = z2+c-1
fc(z) = f(z,c) =f1(f0(z,c),c) =
(z2+c+1)2+c-1.
Derivative: fc‘(z) = 4z(z2+c+1)
Critical points are where fc‘(z) = 0. One critical point is 0, which we have studied in some detail. The other two are the roots of (z2+c+1),
The sign does not matter (it disappears with the first z2), both roots behave the same. So, for today only, let z0 be one of these roots and the starting point for the fractal iteration. Also forget about the two step function for now, and look at the original sequence fractal definition,
and write out the first few iterations (notice the alternating function subscript)
z0,f0(z0,c),
f1(f0(z0,c),c),
f0(f1(f0(z0,c),c),c),
f1(f0(f1(f0(z0,c),c),c), c)…
z0 was defined to be a root of (z2+c+1)=0 which is exactly f0(z,c).
How convenient! We can rewrite the orbit as
z0, 0, f1(0,c),
f0(f1(0,c),c),
f1(f0(f1(0,c),c),c)…
After the first step this is exactly the sequence fractal for si = -1, 1, -1, 1, … starting at 0. That sequence will be the subject of the next several posts.